Constructing a regular hexdecagon (16-sided polygon) using a compass and straightedge
Constructing a tetradecagon (14 sided polygon) with a straightedge and compass
Guess which Aussies will soon be, effectively, on an 85% marginal tax rate?
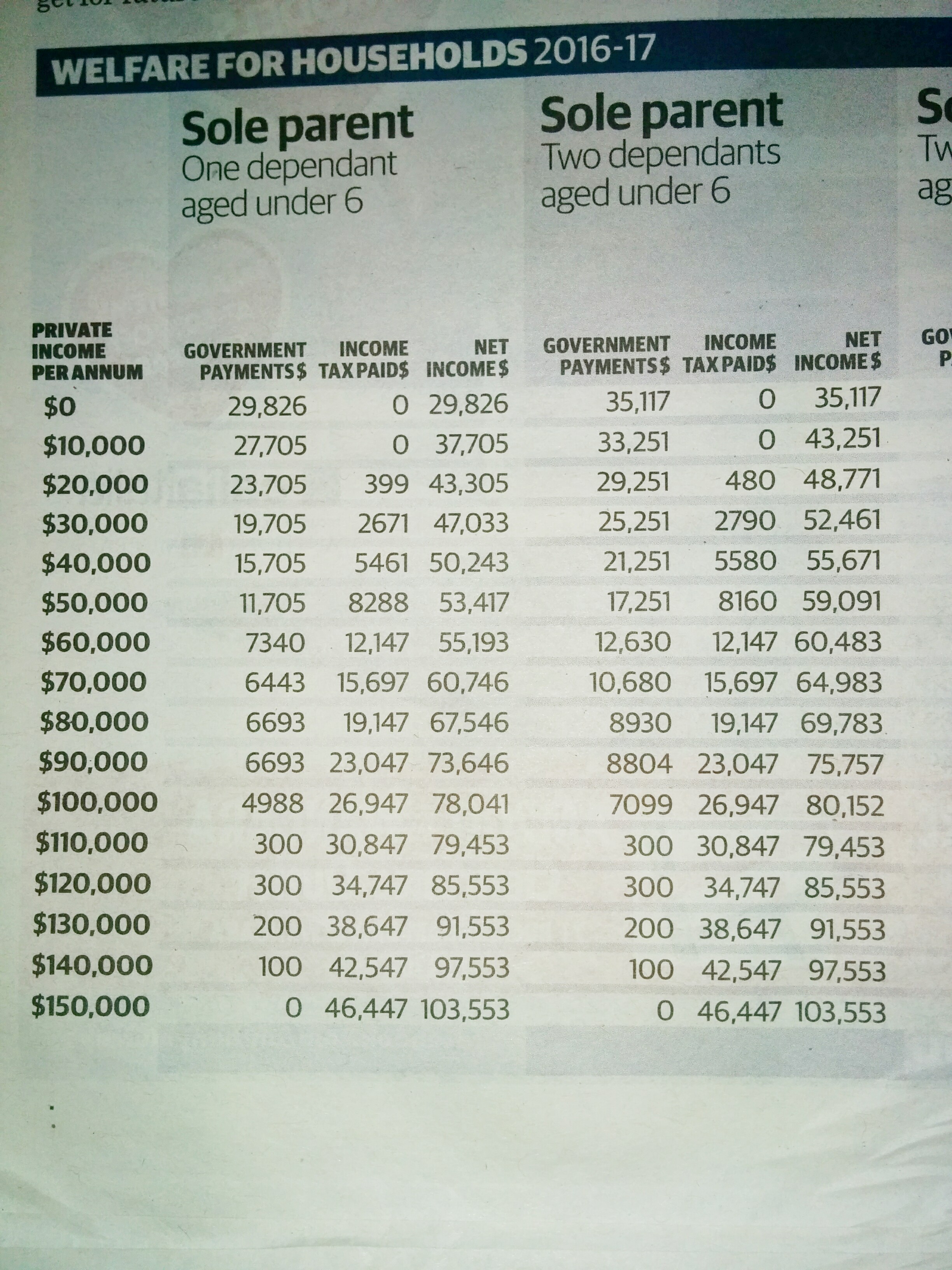
Guess which Aussies will soon be, effectively, on an 85% marginal tax rate?
That’s right, it’s single parents of young kids, earning between 50k to 60k.
Four every extra dollar they earn, they’ll keep a whopping great 13.9 cents.
Share their pain!
Constructing a tridecagon (triskaidecagon) in a circumcircle with ruler and compass
Constructing a regular dodecagon in a circumcircle
Learn to do the impossible in this video!
Learn to do the impossible in this video!
Very nice animation

Very nice animation
Originally shared by Malin Christersson
Ideal Triangles
When using the Poincaré disc model for hyperbolic geometry, the hyperbolic universe is inside a circle. The circle itself is at infinity. A triangle inside the circle will always have angle sum less than 180 degrees. As the vertices of a triangle approach the circle, the angle sum tends to 0, and the hyperbolic perimeter of the triangle tends to infinity. The limiting triangle is called an ideal triangle. The hyperbolic area of an ideal triangle is always π. All triangles in the animation have the same hyperbolic area.
(This is actually a remake of an old post, but since Python is no longer supported in GeoGebra beta, I’m remaking some old stuff linked to non-Euclidean geometry that I never bundled to anything useful before.)